| Sorting Slides
Description Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible. The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written. 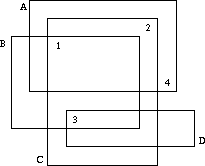 Input The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input. This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary. The input is terminated by a heap description starting with n = 0, which should not be processed. Output For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier. If no matchings can be determined from the input, just print the word none on a line by itself. Output a blank line after each test case. Sample Input 46 22 10 204 18 6 168 20 2 1810 24 4 89 1519 1711 721 1120 2 0 20 2 0 21 11 10 Sample Output Heap 1(A,4) (B,1) (C,2) (D,3)Heap 2none Source |
大致题意:
如图,给出n个方块左上角的坐标和右下角的坐标,再给出4个数字的坐标。已知每个数字唯一的属于一个方块,求出哪些数字和方块的对应关系是必须确定的。 大致思路:
首先按照数字和方块的对应关系建立二分图(比如上图中1对应ABC,2对应AC,3对应BCD,4对应A),然后依次试着删去这些关系,再求最大匹配。如果匹配数少于n则说明这个关系必须存在。
#include#include #include using namespace std;const int N=110;int n,map[N][N],x[N][2],y[N][2],num[N][2];int linker[N],vis[N];int DFS(int u){ int v; for(v=1;v<=n;v++) if(map[u][v] && !vis[v]){ vis[v]=1; if(linker[v]==-1 || DFS(linker[v])){ linker[v]=u; return 1; } } return 0;}int Hungary(){ int u,ans=0; memset(linker,-1,sizeof(linker)); for(u=1;u<=n;u++){ memset(vis,0,sizeof(vis)); if(DFS(u)) ans++; } return ans;}int main(){ //freopen("input.txt","r",stdin); int cases=0; while(~scanf("%d",&n) && n){ memset(map,0,sizeof(map)); for(int i=1;i<=n;i++) scanf("%d%d%d%d",&x[i][0],&x[i][1],&y[i][0],&y[i][1]); for(int i=1;i<=n;i++) scanf("%d%d",&num[i][0],&num[i][1]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(num[i][0]>=x[j][0] && num[i][0]<=x[j][1] && num[i][1]>=y[j][0] && num[i][1]<=y[j][1]) map[i][j]=1; printf("Heap %d\n",++cases); int flag=0; for(int j=1;j<=n;j++) for(int i=1;i<=n;i++){ if(map[i][j]==0) continue; map[i][j]=0; if(Hungary()